Simple or Log Returns?
One thing that puzzles many in quantitative finance
is when log return is appropriate and when simple return should be used.
While there are several benefits of using log returns like log-normality,
time additiveness, approximate raw-log equality and mathematical ease, a common
fallacy is to use is at places where it is not appropriate. The most important
difference between simple and log returns is the features of time-additivity
and asset-Additivity.
Simple
returns are asset-additive: Portfolio return is
the weighted average of the stocks in the portfolio.
where weights are the
proportion of an individual stock in the portfolio and the sum of the weights
is 1. Therefore, if an investor puts an equal amount of money in each stock it
will be called “equally-weighted” portfolio. The return of an equally-weighted
portfolio is just the average return of all stocks in the portfolio.
On the contrary, if investment in each stock is in proportion to
its total outstanding market shares it is termed as “value-weighted” portfolio,
where the weight of an asset is equal to
the proportion of its value to the total value of all assets in the portfolio.
A value-weighted portfolio is more realistic and easy to maintain as no
frequent rebalancing is required.
Log
returns are not asset-additive. The weighted average of log returns of
individual stocks is not equal to the
portfolio return. In fact, log returns
are not a linear function of asset weights. In comparison, if simple returns
are used than the portfolio return is the weighted average of assets in that
portfolio. So one of the advantages of
simple return is that it can be used where portfolios are formed and portfolio
returns have to be calculated because of its asset-additive property.
Log
returns are time-additive: The logarithmic return
of an asset over a period of t to T is the sum of all logarithmic returns
between the t and T. In other words, the log return over n
periods is merely the difference in log between initial and final periods. This
is an advantage because the sum of a
normally distributed variable is also normally-distributed.
This is a negative feature of simple returns as probability
theory states that the product of normally distributed variables is not normally-distributed.
Takeaways:
1. When a cross-section of assets is being studied use simple returns
Reference:
1. Campbell, J. Y., Lo, and A. W., MacKinlay (2007). The econometrics of financial markets. PrincetonUniversity Press, Princeton, New Jersey.
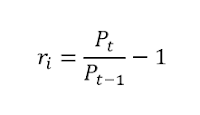


Thanks Dr. Tariq Aziz for sharing the article..
ReplyDeleteuseful thank you
ReplyDeletethank u
ReplyDeleteHello, I dont suppose you know the answer to this... if you are using log returns in the capital asset pricing model, does the risk-free rate also need to be in log returns?
ReplyDelete
ReplyDeleteunder what circumstances log returns can be problematic for measuring portfolio performance?
common stock value calculator
ReplyDeleteIDM Crack
ReplyDeletehistorical stock value calculator